Movimento Uniformente Variado

Predefinição:Mecânica Clássica 'Movimento uniformemente variado' é o movimento no qual a velocidade escalar varia uniformemente no decorrer do tempo. O movimento caracteriza-se por haver uma aceleração escalar constante e diferente de zero.

Função horária da velocidade

A equação da velocidade em função do tempo é:

$v=v_0+\alpha t$

onde:

$v$ (ou $v(t)$) é a velocidade no momento $t$;
$v_0$ é a velocidade inicial. Caso o instante inicial seja $t=0$, teremos $v_0=v(0)$;
$\alpha$ é a aceleração; e
$t$ é o tempo decorrido desde o início do movimento.

Como a aceleração escalar é a mesma em todos os instantes, ela coincide com a aceleração escalar média, qualquer que seja o intervalo de tempo considerado.

Então escrevemos:

$\alpha =\frac{\mathrm{\Delta }v}{\mathrm{\Delta }t}\Rightarrow \alpha =\frac{v-v_0}{t-0}\Rightarrow v=v_0+\alpha t$

Essa função estabelece como varia a velocidade escalar no percorrer do tempo no movimento uniformemente variado:$v_0$ e $\alpha$ são constantes, e a cada valor de $t$ corresponde um único valor de $v$

Na tabela a seguir vemos alguns exemplos, considerando a velocidade $v$ em metros por segundo (m/s) e a aceleração $\alpha$ em metros por segundo ao quadrado.

$v=v_0+{\alpha }_t$	$v_0$	$\alpha$
v = 5 + 2t	$v_0$ = +5 m/s	$\alpha$ = +2 m/s²
v = -3 + 8t	$v_0$ = -3 m/s	$\alpha$ = +8 m/s²
v = 2 + 3t	$v_0$ = 2 m/s	$\alpha$ = +3 m/s²
v = 2 - 3t	$v_0$ = +2 m/s	$\alpha$ = -3 m/s²
v = -4 - 9t	$v_0$ = -4 m/s	$\alpha$ = -9 m/s²

Função horária do espaço

A equação que fornece a posição do móvel em qualquer instante t é:

$s=s_0+v_{0}t+\frac{\alpha }{2}{t}^2$

A fórmula acima é obtida integrando-se a função horária da velocidade:

$\mathrm{\Delta }s=\int v(t)dt=\int (v_0+\alpha t)dt\Rightarrow s-s_0=v_{0}t+\frac{\alpha }{2}{t}^2\Rightarrow s=s_0+v_{0}t+\frac{\alpha }{2}{t}^2$

onde $s$ é a posição (distância) atual do corpo (o s vem do latim spatio, mas também é utilizada o d, por indicar distância), $s_0$ é a posição da qual ele começou o movimento, $v_0$ é a velocidade inicial do corpo, $a$ é a aceleração e $t$ é o tempo decorrido desde o início do movimento. Na função horária do MUV, o coeficiente de $t^2$ é $\frac{\alpha }{2}$.

Assim , se a função for do tipo: $s=5+2t+4t^2$ (s em metros e t em segundos) , observaremos que:

$4=\frac{\alpha }{2}\Rightarrow \alpha =2\cdot 4\Rightarrow \alpha =8\text{ m/s²}$

Portanto , para se ter a aceleração escalar $\alpha$ basta multiplicarmos o coeficiente de $t^2$ por 2. Obtemos assim:

Movimento Uniformemente Variado
$s=s_0+v_{0}t+\frac{\alpha }{2}{t}^2$      $v=v_0+\alpha t$       $\alpha =constante\ne 0$

Essas funções têm o papel de definir o MUV em qualquer trajetória. No entanto apenas o conhecimento dessas, não permite nenhuma conclusão sobre a forma da trajetória.

Da função horária após identificarmos $s_0$, $v_0$ e $\alpha$ , podemos chegar à função horária da velocidade escalar, como vemos no exemplo:

$s=\underset{\downarrow }{s_0}+\underset{\downarrow }{v_{0}t}+\underset{\downarrow }{\frac{\alpha }{2}}{t}^2\underset{\text{ligando-se à função horária de v}}{\overset{v}{\to }}v=v_0+\alpha t$

$\underset{Fs}{\underbrace{s=5-2t+\frac{3}{2}{t}^2}}$ $\Rightarrow$ $Temos:s_0=5m;v_0=-2m/s;\alpha =3m/s^2\Rightarrow \underset{Fv}{\underbrace{v=-2+3t}}$

Perceba que da função horária dos espaços (Fs) chega-se à função horária da velocidade , representada por (Fv).

Equação de Torricelli no MUV

No MUV há muitos casos em que podemos relacionar a velocidade escalar v em função do espaço s o que é feito com o emprego da equação de Torricelli que mostra-se a seguir:

$v^2=v_0^2+2\alpha t{v}_0+{\alpha }^2{t}^2\Rightarrow v^2=v_0^2+2\alpha (v_{0}t+\frac{\alpha }{2}{t}^2)$

Comparando com a função horária ...

$s-s_0=v_{0}t+\frac{\alpha }{2}{t}^2,temos:v^2=v_0^2+2\alpha (s-s_0)$

ou ainda:

$v^2=v_0^2+2a\mathrm{\Delta }s$ equação de Torricelli para o MUV

onde $v$ é a velocidade atual, $v_0$ é a velocidade inicial, $a$ é a aceleração e $\mathrm{\Delta }s$ é a variação de posição durante o movimento.Sabendo-se que as variações são iguais a zero (...) Nessa fórmula, a velocidade escalar varia em função do espaço; $v_0$ é a velocidade inicial, e $\alpha$ é a aceleração escalar do movimento, podendo ser positiva ou negativa de acordo com as convenções adotadas.

Velocidade média

A velocidade média no MUV é dada pela média aritmética entre a velocidade final e inicial:

$\bar{v}=\frac{\mathrm{\Delta }S}{\mathrm{\Delta }t}=\frac{v_0+v_f}{2}=v_0+\frac{at}{2}$

Gráficos do MUV

Gráfico da velocidade em função do tempo

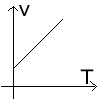
No movimento uniformemente variado podemos perceber três funções distintas:

1. Aceleração em função do tempo - Como a aceleração nesse movimento é constante e diferente de zero, então apresenta-se uma função constante. Logo o gráfico apresenta-se como uma reta paralela ao eixo das abscissas.
2. Velocidade em função do tempo - A função da velocidade em função do tempo é uma função de primeiro grau. Logo apresenta-se como uma linha reta que concorre com o eixo das abscissas.
3. Deslocamento em função do tempo - O deslocamento em função do tempo é uma função de segundo grau. Logo ela se apresenta como uma parábola.